This is an old revision of the document!
Table of Contents
GeoDMA 2.0 Features
GeoDMA has metrics integrating Polygons, Cells, and Images. Through image segmentation, GeoDMA creates Polygons.
We provide a list of 3 feature types, including:
- Segmentation-based spectral features
- Segmentation-based spatial features
- Landscape-based features
Segmentation-based spectral features
All spectral metrics are calculated inside a polygon, when  , or inside a cell, when
, or inside a cell, when  The spectral channel is defined by
The spectral channel is defined by 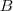 , and the total number of bands is defined by
, and the total number of bands is defined by 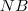 .
.
Some of the following equations describe features based on the Gray-Level Cooccurrence Matrix - GLCM. The term 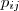 is the normalized frequency in which two neighboring cells separated by a fixed shift occur on the image, one with gray tone
is the normalized frequency in which two neighboring cells separated by a fixed shift occur on the image, one with gray tone  and the other with gray tone
and the other with gray tone 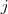 . The constant
. The constant 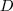 is the dimension of the GLCM, which has the same gray value range of the original image.
is the dimension of the GLCM, which has the same gray value range of the original image.
| Name | Description | Formula | Range | Units |
| AMPLITUDE_BAND | Defines the amplitude of the pixels inside the object. The amplitude means the maximum pixel value minus the minimum pixel value. | 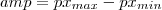 |  | 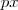 |
| BAND_RATIO_BAND | Describes the contribution of the given band to the region. | 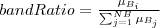 |  | 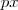 |
| COUNT_BAND | Defines the total number of pixels inside the object, including pixels with dummy values. | 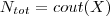 |  | 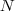 |
| CONTRAST_SE_BAND | Returns a measure of the intensity contrast between a pixel and its southeast neighbor over the object. Contrast is 0 for a constant object. It is also known as Sum of Squares Variance | 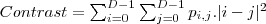 | ![Math $[0, (size(GLCM, 1)-1)^2]$](/lib/exe/fetch.php?media=wiki:latex:/imge04e0ecd3195662c93bae8b7cd5e2450.png) | - |
| DISSIMILARITY_SE_BAND | Measures how different the elements of the GLCM are from each other and it is high when the local region has a high contrast. | 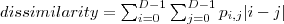 |  | - |
| ENERGY_SE_BAND | It returns the squared root of Angular Second Moment, computed by the sum of the squared elements in GLCM. Energy is 1 for a constant image. | 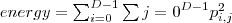 | ![Math $[0,1]$](/lib/exe/fetch.php?media=wiki:latex:/imgacf5ce819219b95070be2dbeb8a671e9.png) | - |
| ENTROPY_SE_BAND | Measures the disorder in an image. When the image is not uniform, many GLCM elements have small values, resulting in large entropy. | 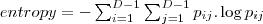 |  | - |
| HOMOGENEITY_SE_BAND | Assumes higher values for smaller differences in the GLCM. Also called Inverse Difference Moment. Homogeneity is 1 for a diagonal GLCM. | 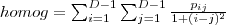 |  | - |
| KURTOSIS_BAND | Returns the kurtosis value for all the valid pixels (not dummy) inside the object. | 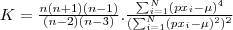 | 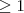 | - |
| MAXIMUM_VAL_BAND | Computes the maximum gray level value (not dummy) inside the object. | 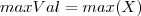 | 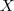 | 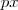 |
| MEAN_BAND | Computes the average value for all 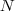 pixels inside the object. pixels inside the object. | 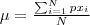 |  | 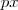 |
| MEDIAN_BAND | Computes the median for all 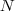 pixels inside the object. pixels inside the object. | 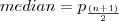 | 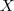 | 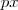 |
| MINIMUM_VAL_BAND | Computes the minimum gray level value (not dummy) inside the object. | 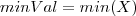 | 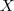 | 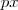 |
| MODE_BAND | Returns the most occurring gray level value (mode) for all  (not dummy) pixels inside the object. When the object is multimodal, the first value is assumed. (not dummy) pixels inside the object. When the object is multimodal, the first value is assumed. | 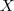 | 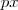 |
|
| NUM_MODES_BAND | Returns the number of modes for the object. | 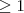 | 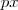 |
|
| SKEWNESS_BAND | Returns the skewness value for all the valid pixels (not dummy) inside the object. | 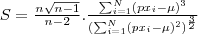 | - | - |
| STD_DEVIATION_BAND | Returns the standard deviation of all 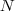 (not dummy) pixels ( (not dummy) pixels (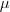 is the mean value) inside the object. is the mean value) inside the object. | 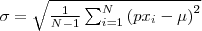 |  | 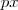 |
| SUM_BAND | Returns the sum of all 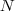 (not dummy) pixels inside the object. (not dummy) pixels inside the object. | 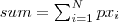 |  | 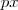 |
| VALID_COUNT_BAND | Defines the total number of pixels inside the object with not dummy values. | 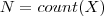 |  |  |
| VAR_COEFF_BAND | Returns the coefficient of variation of the values for all the valid pixels (not dummy) inside the object | 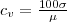 | ![Math $[0,100]$](/lib/exe/fetch.php?media=wiki:latex:/imgfab8fdd23a02acf1114ba427cc593d52.png) | % |
| VARIANCE_BAND | Returns the variance of all  (not dummy) pixels ( (not dummy) pixels (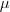 is the mean value) inside the object. is the mean value) inside the object. | 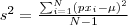 |  | 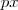 |
Segmentation-based spatial features
| Name | Description | Formula | Range | Units |
| POL_ANGLE | Represents the main angle of an object. It is obtained by computing the minimum circumscribing ellipse, and the angle of the biggest radius of the ellipse suits to the object's angle. | ![Math $\left[-\pi, \pi]$](/lib/exe/fetch.php?media=wiki:latex:/imgca12761e2ef3bd0616af061afcdd5cd6.png) | 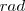 |
|
| POL_AREA | Returns the area of the object, measured in the unit of measure of the current Spatial Reference System. |  | ![Math $[m,degrees,...]^2$](/lib/exe/fetch.php?media=wiki:latex:/img706095e1c1a07ec3cdf4a1f54368ab5e.png) |
|
| POL_BBOX_AREA | Returns the bounding box area of an object, measured in the unit of measure of the current Spatial Reference System. |  | ![Math $[m,degrees,...]^2$](/lib/exe/fetch.php?media=wiki:latex:/img706095e1c1a07ec3cdf4a1f54368ab5e.png) |
|
| POL_BBOX_PERIM | Returns the perimeter of the bounding box of an object, measured in the unit of measure of the current Spatial Reference System. |  | ![Math $[m,degrees,...]$](/lib/exe/fetch.php?media=wiki:latex:/img2a0354016e418bf92250573f2241fead.png) |
|
| POL_CIRCLE | Relates the areas of the object and the smallest circumscribing circle around the object. In the equation, 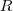 is the maximum distance between the centroid and all vertices. is the maximum distance between the centroid and all vertices. | 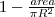 | 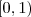 | ![Math $[m,degrees,...]^2$](/lib/exe/fetch.php?media=wiki:latex:/img706095e1c1a07ec3cdf4a1f54368ab5e.png) |
| POL_ELLIPTIC_FIT | Finds the minimum circumscribing ellipse to the object and returns the ratio between the object's area and the ellipse area. | ![Math $\left[0, 1\right]$](/lib/exe/fetch.php?media=wiki:latex:/img6361058cb575f97ea02929e18860d18e.png) | - | |
| POL_FRACTALDIM | Returns the fractal dimension of an object. | 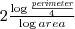 | ![Math $[1, 2]$](/lib/exe/fetch.php?media=wiki:latex:/imge5c1eec8f3fd45f8ee7a07bdef6ceac6.png) | - |
| POL_GYRATION_RATIUS | This feature is equals the average distance between each vertex of the polygon and it's centroid. The more similar to a circle is the object, the more likely the centroid will be inside it, and therefore this feature will be closer to 0. | 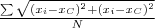 |  | ![Math $[m, degrees, ...]$](/lib/exe/fetch.php?media=wiki:latex:/img6af70905a5e7efccc935cb68d5afd9b5.png) |
| POL_BBOX_LENGTH | It is the height of the object's bounding box, measured in the unit of measure of the current Spatial Reference System. |  | ![Math $[m, degrees, ...]$](/lib/exe/fetch.php?media=wiki:latex:/img6af70905a5e7efccc935cb68d5afd9b5.png) |
|
| POL_PERIMETER | Returns the perimeter of the object, measured in the unit of measure of the current Spatial Reference System. |  | ![Math $[m,degrees,...]$](/lib/exe/fetch.php?media=wiki:latex:/img2a0354016e418bf92250573f2241fead.png) |
|
| POL_PERIM_AREA_RATIO | Calculates the ratio between the perimeter and the area of an object. | 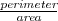 |  | 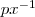 |
| POL_RECTANGULAR_FIT | This feature fits a minimum rectangle outside the object and calculates the ratio between its area and the area of this rectangle. The closer to  is this feature, the most similar to a rectangle. is this feature, the most similar to a rectangle. | 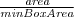 | ![Math $\left[0, 1\right]$](/lib/exe/fetch.php?media=wiki:latex:/img6361058cb575f97ea02929e18860d18e.png) | - |
| POL_BBOX_WIDTH | Returns the width of the object's bounding box, measured in the unit of measure of the current Spatial Reference System. |  | ![Math $[m, degrees, ...]$](/lib/exe/fetch.php?media=wiki:latex:/img6af70905a5e7efccc935cb68d5afd9b5.png) |
|
| POL_COMPACITY | Returns the compacity of the object. | 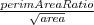 |  | - |
| POL_DENSITY | This feature corresponds to the ratio between the polygon area and the polygon radius. | 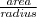 |  | - |
| POL_SHAPE_INDEX | This feature corresponds to the ratio between the polygon perimeter and the squared root of the polygon area. | 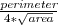 |  | - |
Landscape-based features
When the unit is hectares, the value is divided by 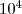 . Please note that most of the following features are based on Fragstats software.
. Please note that most of the following features are based on Fragstats software.
| Name | Description | Formula | Range | Units |
| c_CA | Class Area means the sum of areas of a given class inside a cell. | 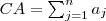 |  | 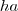 |
| c_PERCENTLAND | 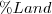 equals the sum of the areas ( equals the sum of the areas (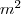 ) of all patches of the corresponding patch type (class), divided by total landscape area ( ) of all patches of the corresponding patch type (class), divided by total landscape area (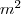 ). ). 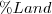 is equals to the percentage the landscape comprised of the corresponding patch type (class). is equals to the percentage the landscape comprised of the corresponding patch type (class). | 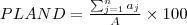 | ![Math $\left[0, 100\right]$](/lib/exe/fetch.php?media=wiki:latex:/img344086ee06bcdffe5ca970535fb2e131.png) | 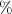 |
| c_PD | PD stands for Patch Density, which is equals the number of patches in the landscape, divided by total landscape area (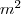 ), multiplied by 10,000 and 100 (to convert to 100 hectares). Note, PD does not include background patches or patches in the landscape border, if present. However, total landscape area ( ), multiplied by 10,000 and 100 (to convert to 100 hectares). Note, PD does not include background patches or patches in the landscape border, if present. However, total landscape area (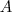 ) includes any internal background present. ) includes any internal background present. | 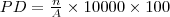 |  | Number/100ha |
| c_MPS | MPS stands for Mean Patch Size, which is equals to the sum of the areas (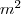 ) of all patches of the corresponding patch type, divided by the number of patches of the same type. ) of all patches of the corresponding patch type, divided by the number of patches of the same type. | 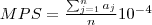 |  | 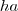 |
| c_PSSD | PSSD stands for Patch Size Standard Deviation, which is the root mean squared error (deviation from the mean) in patch size. This is the population standard deviation, not the sample standard deviation. | 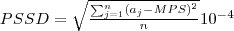 |  | 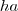 |
| c_LSI | LSI stands for Landscape Shape Index, which is equals the sum of the landscape boundary and all edge segments (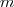 ) within the boundary. This sum involves the corresponding patch type (including borders), divided by the two times the square root of the total landscape area ( ) within the boundary. This sum involves the corresponding patch type (including borders), divided by the two times the square root of the total landscape area (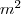 ) multiplied by pi ( ) multiplied by pi (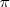 ). ). | 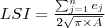 | 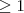 | - |
| c_MSI | MSI stands for Mean Shape Index, which is equals the sum of the patch perimeter (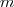 ) by divided two times the square root of patch area ( ) by divided two times the square root of patch area (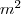 ) multiplied by pi ( ) multiplied by pi (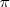 ) for each patch of the corresponding patch type, divided by the the number of patches of the same patch type (class). ) for each patch of the corresponding patch type, divided by the the number of patches of the same patch type (class). | 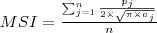 | 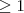 | - |
| c_AWMSI | AWMSI stands for Area-Weighted MSI, which is equals the sum of the landscape boundary and all edge segments (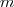 ) within the boundary. This sum involves the corresponding patch type (including borders), divided by the two times the square root of the total landscape area ( ) within the boundary. This sum involves the corresponding patch type (including borders), divided by the two times the square root of the total landscape area (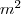 ) multiplied by pi ( ) multiplied by pi (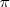 ). This first term is multiplied by the area of the corresponding patch, divided by the sum of the areas of all patches of the same patch type (class). ). This first term is multiplied by the area of the corresponding patch, divided by the sum of the areas of all patches of the same patch type (class). | ![Math $AWMSI = \sum_{j=1}^n \left[ \frac{p_j}{2 \sqrt{\pi \times a_j}} \times \frac{a_j}{\sum_{j=1}^n a_j} \right]$](/lib/exe/fetch.php?media=wiki:latex:/img4ea146fd0403554ca84c268f8af0e37f.png) | 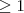 | - |
| c_MPFD | MPFD stands for the Mean Patch Fractal Dimension. | 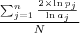 | ||
| c_AWMPFD | AWMPFD stands for Area-weighted Mean Patch Fractal Dimension. | ![Math $\sum_{j = 1}^{n} [\frac{2 \times \ln{p_j}}{\ln{a_j}} \times \frac{a_j}{\sum_{j = 1}^{n} a_{ij}}}]$](/lib/exe/fetch.php?media=wiki:latex:/imge037888c83cba9f30fdd89c2e3af6f1b.png) | ||
| c_ED | Edge Density equals the sum of the lengths (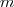 ) of all edge segments involving the corresponding patch type, divided by the total landscape area ( ) of all edge segments involving the corresponding patch type, divided by the total landscape area (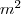 ). ). | 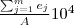 |  | 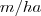 |
| c_MPAR | Mean Perimeter Area Ratio equals the sum of ratios between perimeters and areas, divided by the number of patches of the same type. | 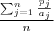 |  | 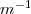 |
| c_PSCOV | Patch Size Coefficient of Variation calculates the ratio between the features c_PSSD and c_MPS. | 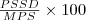 |  | - |
| c_NP | NP stands for Number of Patches, which is equals to the number of patches of a corresponding patch type (class) inside a particular landsacape. | 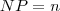 |  | - |
| c_TE | TE equals the total size of the edge. | 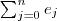 |  | 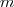 |
| c_IJI | IJI stands for Interspersion and Juxtaposition Index. The observed interspersion over the maximum possible interspersion for the given number of patch types. It only exists for 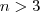 . . | 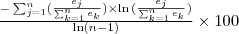 | ![Math $[0, 100]$](/lib/exe/fetch.php?media=wiki:latex:/img0e2109da05f9d8dc33b622fc1001a3c1.png) |  |
| c_TABO | TABO stands for the Total Area of the Biggest Object that intersects the landscape. | 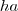 |
||
| PR | PR stands for Patch Richness, which is equals the number of different patch types present within the landscape boundary. | 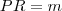 | 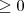 | |
| PRD | PRD stands for Patch Richness Density, which is equals the number of different patch types present within the landscape boundary divided by total landscape area (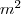 ), multiplied by ), multiplied by 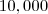 and and 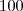 (to convert to (to convert to 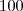 hectares). Note, total landscape area ( hectares). Note, total landscape area (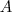 ) includes any internal background present. ) includes any internal background present. | 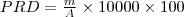 | 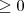 | 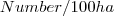 |
| SHDI | SHDI stands for Shannon's Diversity Index, which is equals to minus the sum, across all patch types, of the proportional abundance of each patch type multiplied by that proportion. Note, 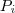 , which is the proportion of the landscape occupied by patch type (class) , which is the proportion of the landscape occupied by patch type (class)  , is based on total landscape area ( , is based on total landscape area (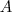 ) excluding any internal background present. ) excluding any internal background present. | 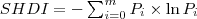 | 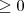 | |
| SIDI | SHDI stands for Simpson's Diversity Index, which is equals to 1 minus the sum, across all patch types, of the proportional abundance of each patch type squared. Note, 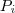 , which is the proportion of the landscape occupied by patch type (class) , which is the proportion of the landscape occupied by patch type (class)  , is based on total landscape area ( , is based on total landscape area (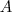 ) excluding any internal background present. ) excluding any internal background present. | 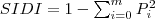 | 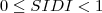 | |
| SHEI | SHEI stands for Shannon's Evenness Index, which is equals to minus the sum, across all patch types, of the proportional abundance of each patch type multiplied by that proportion, divided by the logarithm of the number of patch types. In other words, the observed Shannon's Diversity Index (SHDI) divided by the maximum Shannon's Diversity Index for that number of patch types. Note, 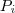 , which is the proportion of the landscape occupied by patch type (class) , which is the proportion of the landscape occupied by patch type (class)  , is based on total landscape area ( , is based on total landscape area (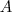 ) excluding any internal background present. ) excluding any internal background present. | 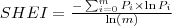 | 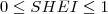 | |
| SIEI | SIEI stands for Simpson's Evenness Index, which is equals to 1 minus the sum, across all patch types, of the proportional abundance of each patch type squared, divided by 1 minus 1 divided by the number of patch types. In other words, the observed Simpson's Diversity Index (SIDI) divided by the maximum Simpson's Diversity Index for that number of patch types. Note, 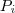 , which is the proportion of the landscape occupied by patch type (class) , which is the proportion of the landscape occupied by patch type (class)  , is based on total landscape area ( , is based on total landscape area (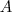 ) excluding any internal background present. ) excluding any internal background present. | 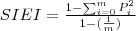 | 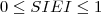 |